Definición
El conjunto de números naturales es el más pequeño dentro de los que son los conjuntos numéricos, son usados para contar u ordenar. Tiene un primer elemento «1», pero no tiene un último elemento, ya que es un conjunto infinito.
Son un subconjunto de los números enteros. No son fraccionarios, ni poseen decimales
Se denotan de la siguiente manera:
ℕ: Conjunto de los números naturales
ℕ = {1,2,3,4,5,6,… + ∞}
Origen de los números naturales
Son los más antiguos que se conocen, ya que nacen de la necesidad de contar y de dar respuesta a la pregunta ¿Cuántos? Este nos permite contar cosas, objetos, personas, entre otras cosas.
Su simbología (N) se debe a la forma natural de contar y ordenar, en el principio solo se conocían unos pocos elementos de este conjunto, incluso en muchas tribus se contaba 1, 2, 3 y luego de esta cantidad se decía «Muchos».
El crecimiento de este conjunto se fue dando a medida que la población iba aumentando.
Existen diversos registros de los estudios de este conjunto, hechos por Egipcios, Indues y Romanos, pero fue en el siglo XIX que Richard Dedekind coloco el conjunto en lo que comenzó a ser una base sólida.
¿Cómo se caracterizan los números naturales?
- Se caracteriza por tener un primer elemento, en este caso 1 E N
- Cada elemento tiene su siguiente, para cualquier número que pertenece a ese conjunto ( n E N), existe su siguiente perteneciente al mismo conjunto ( n+1 E N). Esto quiere decir que 1 + 1 = 2 y 2 pertenece a N, 2 + 1 = 3 y 3 pertenece a N, así sucesivamente
- No hay un último elemento o número, ya que este conjunto es infinito, por ende la sucesión de números naturales es infinita.
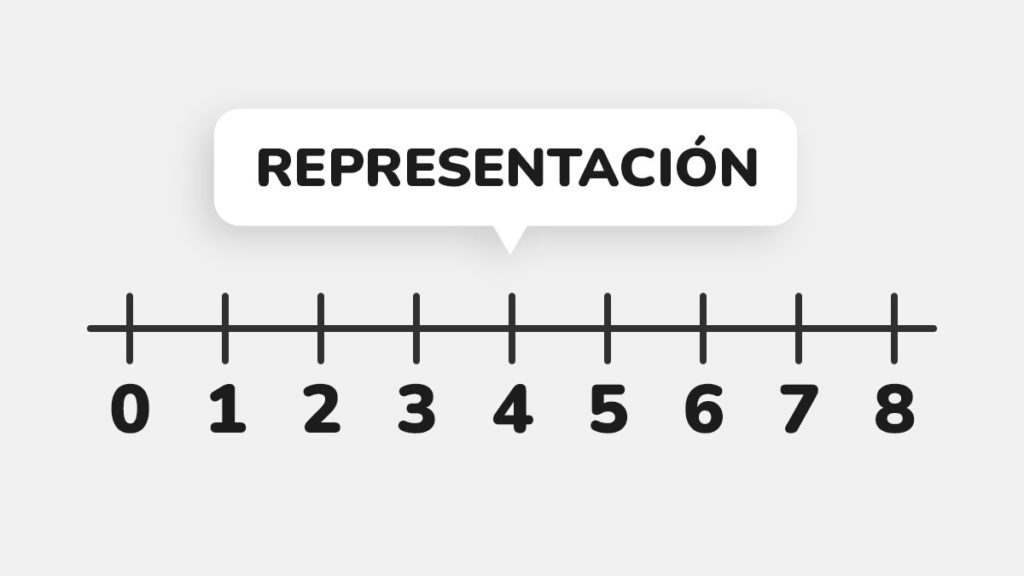
Representación de los números naturales
Para representar se utiliza una semirrecta partiendo del primer elemento (1) como origen de la misma y pequeños segmentos de igual distancia que representan cada elemento en la semirrecta, cabe señalar que cada elemento es único y por ende tendrá una única posición en ella.
Propiedades de los números naturales
Propiedad conmutativa en la adición
Para cualquier elemento que pertenezca al conjunto
a + b = b + a
c = c
Donde a y b se conocen como sumandos y c el resultado final que se conoce como suma. El orden de los elementos o de los sumandos no altera la suma.
Ejemplo:
2 + 3 = 3 + 2
5 = 5
45 + 17 = 17 + 45
62 = 62
Propiedad asociativa en la adición
Para adicionar 3 elementos del conjunto numérico N se tiene que cumplir lo siguiente:
(a + b) + c = a + (b + c)
d = d
Ejemplo:
(2 + 3) + 6 = 2 + (3 + 6)
5 + 6 = 2 + 9
11 = 11
(10 + 35) + 5 = 10 + (35 + 5)
45 + 5 = 10 + 40
50 = 50
Propiedad conmutativa en la multiplicación
El orden de los factores no altera el producto, la multiplicación de dos números naturales cualesquiera es otro número natural
a . b = b . a
c = c
Ejemplo:
5 . 8 = 8 . 5
40 = 40
12 . 6 = 6 . 12
72 = 72
Propiedad asociativa en la multiplicación
El orden de asociar los factores no altera el producto
(a . b) . c = a . (b . c)
d = d
Ejemplo:
(3 . 2) . 7 = 3 . (2 . 7)
6 . 7 = 3 . 14
42 = 42
(10 . 8) . 12 = 10 . (8 . 12)
80 . 12 = 10 . 96
960 = 960

