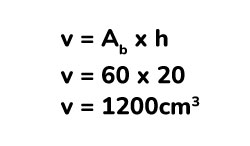¿Qué es un prisma triangular?
Un prisma triangular es un poliedro de tres (3) lados donde su base y superficie están formadas por dos triángulos iguales y paralelos entre sí, sus 3 caras laterales están formadas por rectángulos (paralelogramos).
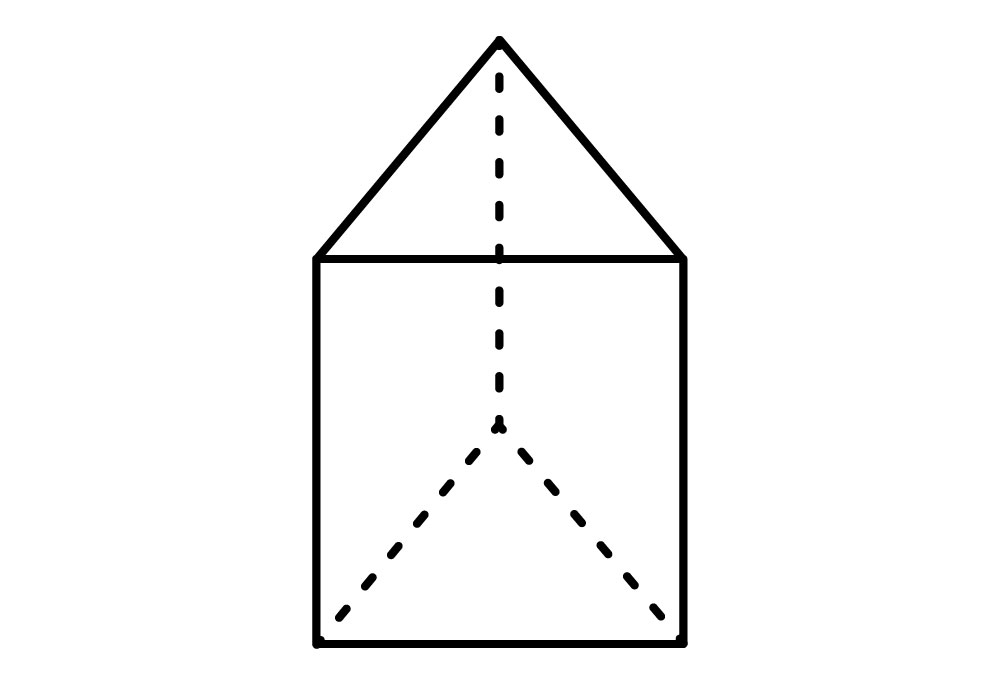
Cómo todo prisma tiene ciertas características que lo definen.
Características de un prisma triangular
- Sus bases son dos triángulos idénticos y paralelos.
- Tiene un total de 5 caras, 2 caras de las bases y 3 caras laterales.
- Tiene 3 caras laterales en forma de rectángulos (paralelogramo) que unen las 2 bases.
- Tiene un total de 6 vértices, que son los puntos donde concurren las caras del prisma.
- Tiene un total de 9 Aristas, que son los segmentos que conforman las caras del prisma.
Tipos de prisma triangular
Regular
Es el prisma que tiene como base un triángulo equilátero.

Irregular
Es aquel que su base es otro triángulo diferente al equilátero.
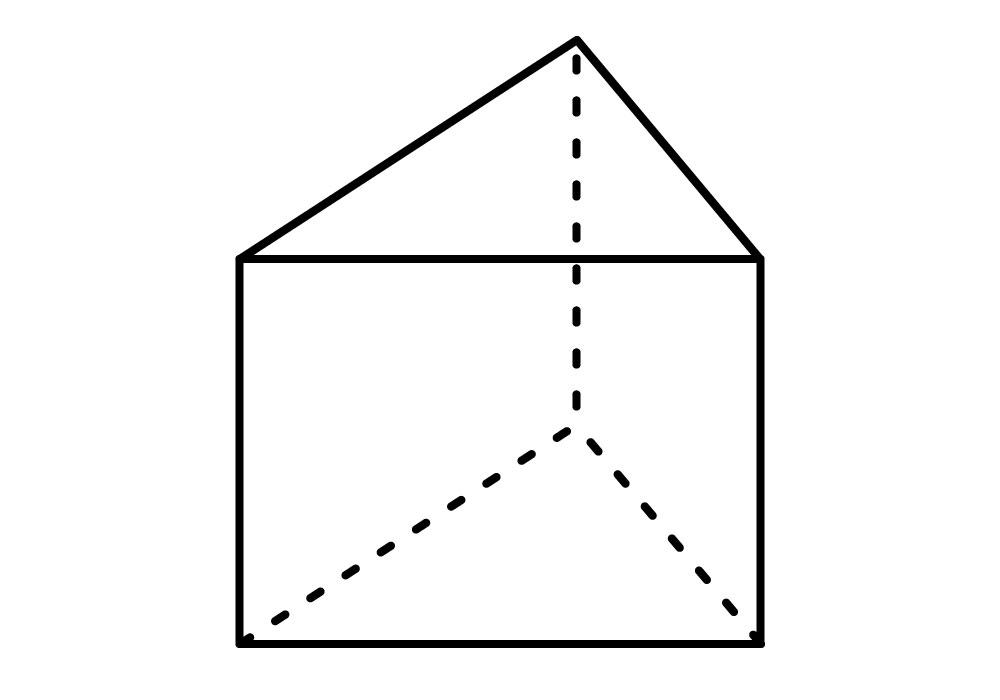
Oblicuo
Es el prisma que sus bases no son paralelas.
También te puede interesar:
Prisma rectangular ¿Qué es? Calcular volumen, área y diagonal.
¿Cómo calcular el área de un prisma triangular?
Para el calcular el área total de un prisma triangular necesitamos saber el área de la base (área del triángulo) que corresponde a la siguiente fórmula.
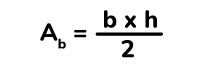
- h = altura del triángulo.
- b = base del triángulo.
Luego el resultado obtenido se multiplica por 2, puesto que tenemos dos triángulos iguales.
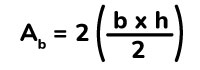
Ahora tenemos que calcular el área de los laterales del prisma triangular con la siguiente fórmula
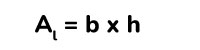
- h = altura del prisma.
- b = base del prisma.
En el caso de prisma triangular regular, el proceso es más sencillo, puesto que son rectángulos que tienen las mismas longitudes. Solamente tendríamos que multiplicar el resultado por 3, quedando así la siguiente fórmula.
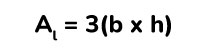
Para el caso del prisma triangular irregular, debemos sacar el área de cada lateral del prisma y luego sumar todos los resultados.
Una vez obtenidos el área de la base y el área de los laterales, lo adicionamos para calcular el área total de prisma triangular. Podemos usar la siguiente fórmula.
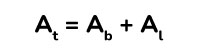
- At = Área total.
- Ab = Área de la base.
- Al = Área de los laterales.
Ejercicio 1
Calcular el área total del prisma triangular regular que está formado por dos y tiene una altura de 15cm, un ancho de 4cm y una altura del triángulo de 2cm.
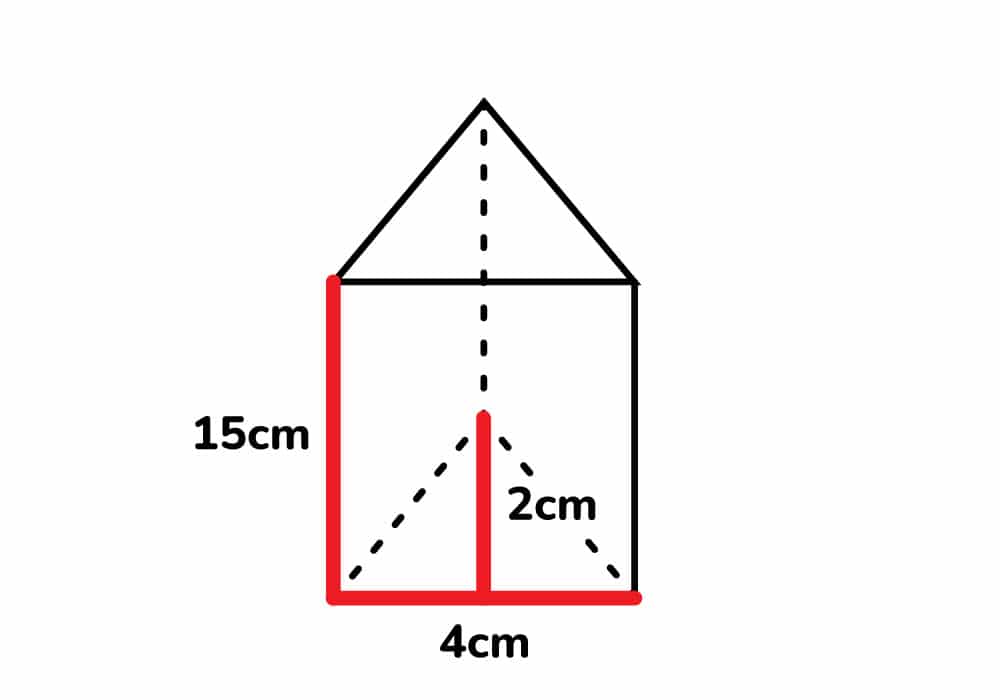
Solución:
Calculamos el área de la base.
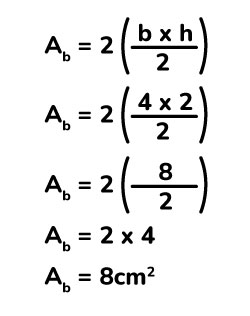
Ahora calculamos el área de los laterales.

Teniendo el área de la base y el área de los laterales, calculamos el área total del prisma.
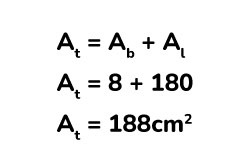
Ejercicio 2
Calcular el área total del prisma que tiene como medida 3cm de base y 10cm de altura.
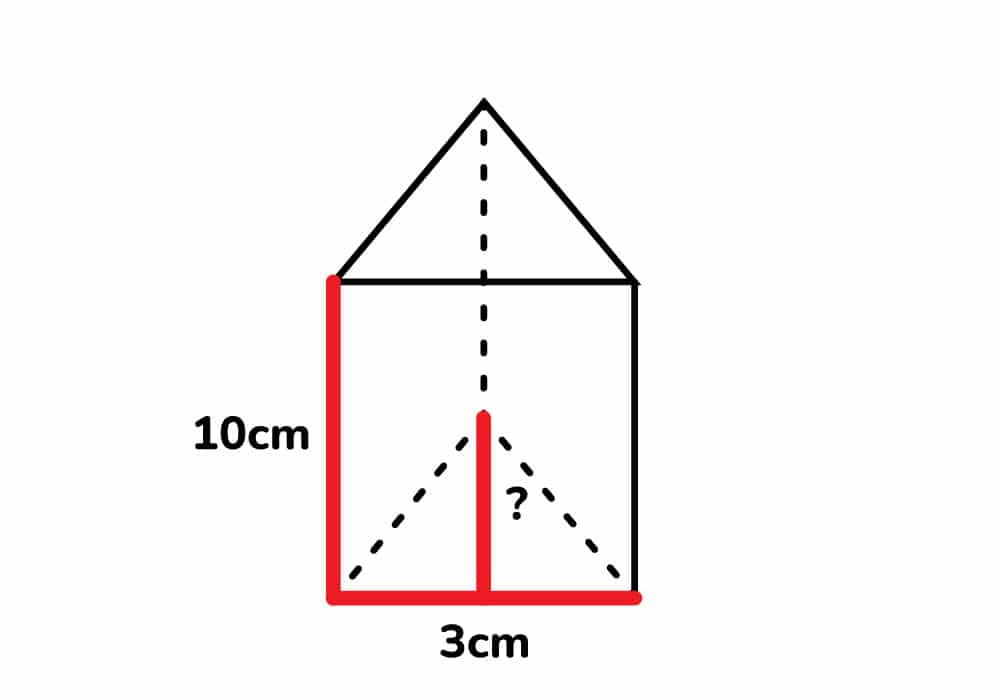
Solución
Como en este caso no tenemos la altura del triángulo, vamos a aplicar el teorema de Pitágoras.
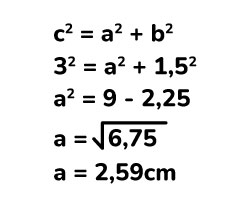
Una vez que tenemos la altura del triángulo procedemos a calcular el área de la base.
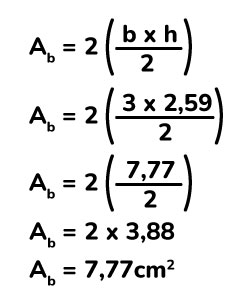
Calculamos el área de los laterales.

Por último, calculamos el área total.
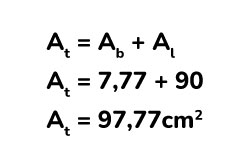
Ejercicio 3
Calcular el área total del siguiente prisma donde sus triángulos tiene dos de sus lados de 6 cm y 1 de 4cm, la altura del mismo es de 3 cm (triángulo isósceles) y el prisma con una altura de 10cm.
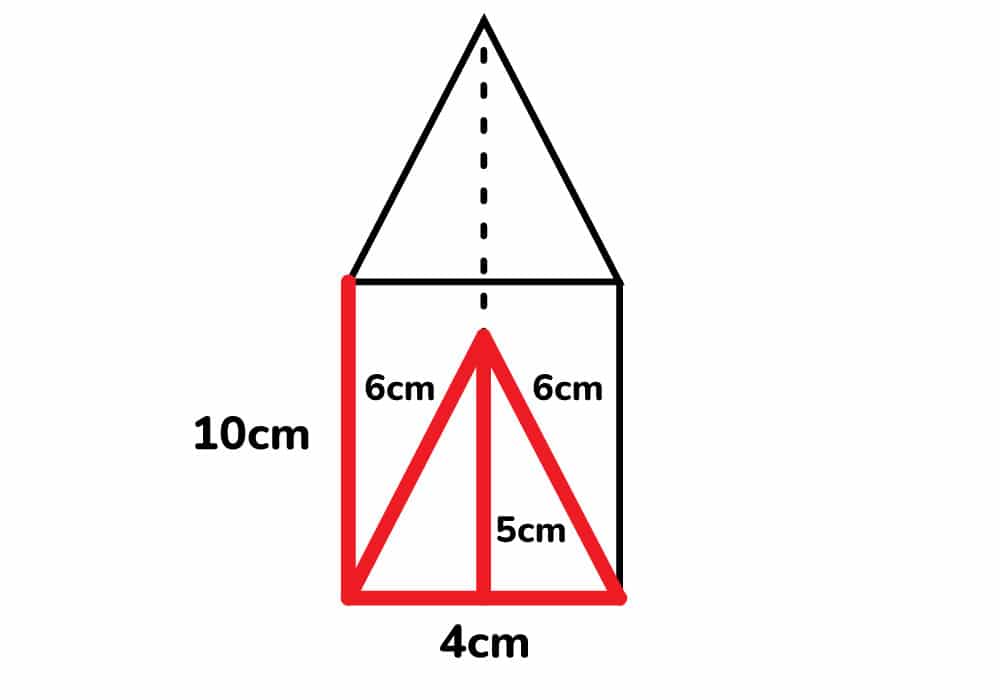
Solución
Calculamos el área de la base.
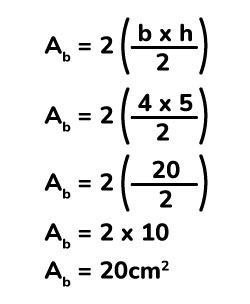
Procedemos ahora a calcular el área de los laterales.
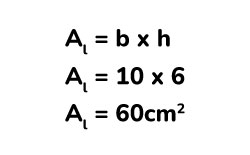
Este resultado lo multiplicamos por 2, puesto que tenemos dos caras laterales idénticas.

Calculamos la cara lateral restante.
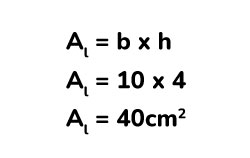
Luego, sumamos todas las áreas calculadas.
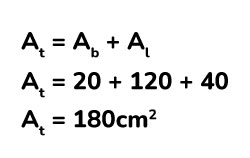
¿Cómo calcular el volumen de un prisma triangular?
El volumen de un cuerpo geométrico es la cantidad de espacio que este ocupa y para calcular el volumen de un prisma triangular debemos conocer el área de la base y la altura del prisma. Esto lo podemos calcular mediante la siguiente fórmula.
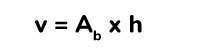
Ejercicio
Calcular el volumen del siguiente prisma triangular, cuyas medidas son las siguientes: 10cm de base, 20 cm de altura del prisma y 12cm la altura del triángulo.
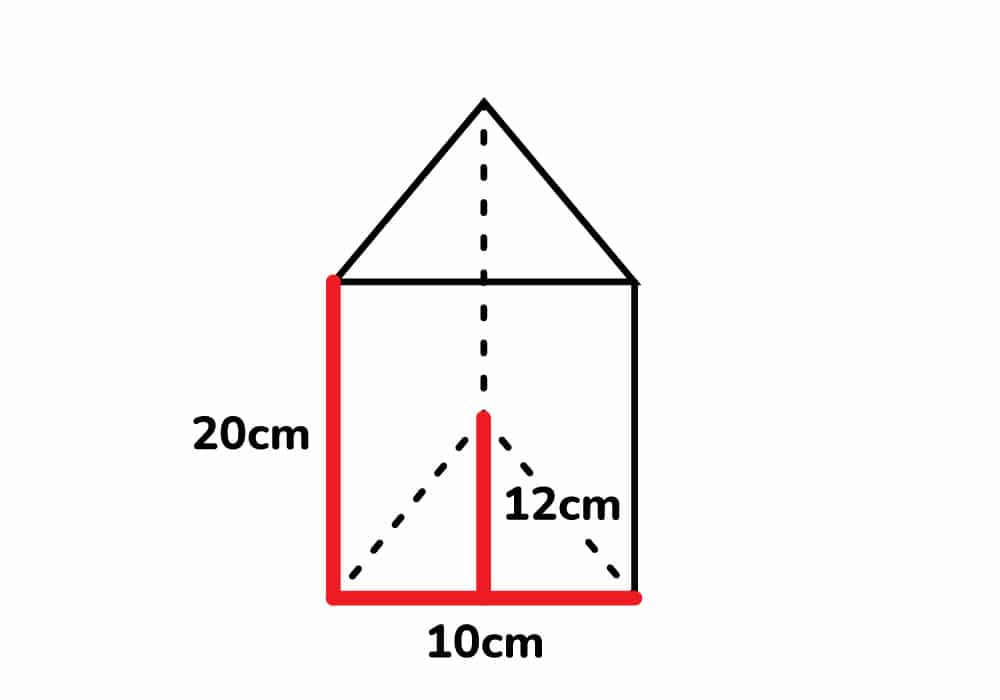
Solución
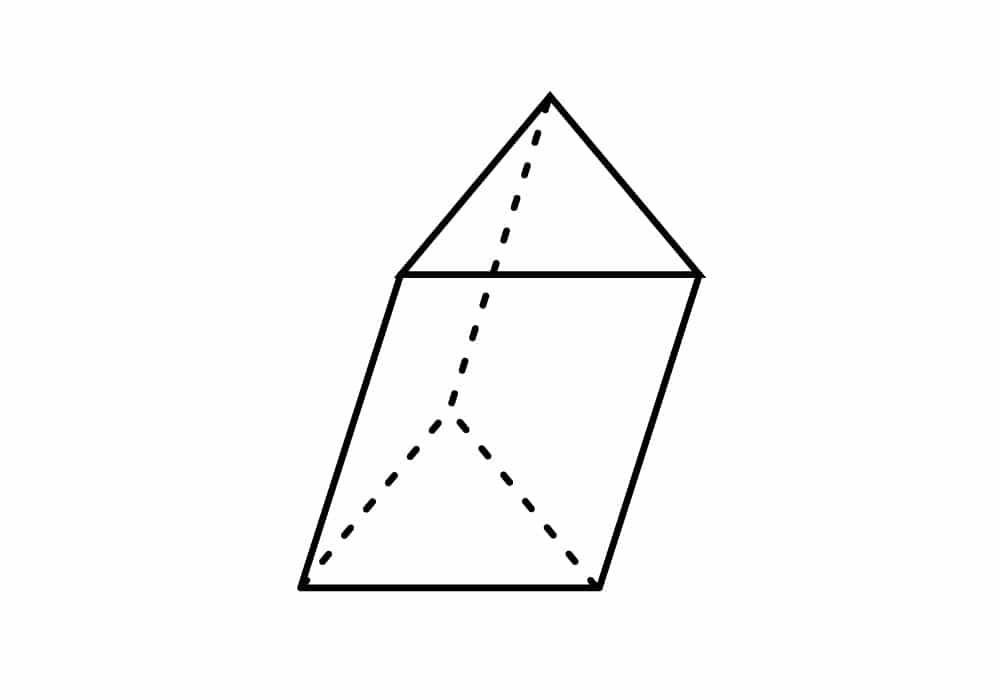
Calculamos el área de la base.
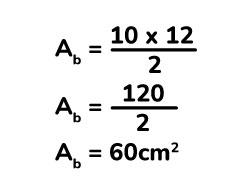
Una vez calculada el área de la base, calculamos procedemos a calcular el volumen.