Ejercicios resueltos de álgebra lineal
El álgebra lineal es una de las ramas fundamentales de las matemáticas que tiene aplicaciones en diversas áreas como la física, la ingeniería, la informática y más. Aquí en Matemante, te ofrecemos una selección de ejercicios resueltos de álgebra lineal para que puedas practicar y mejorar tus habilidades. Este artículo te proporcionará una guía clara y concisa, con ejemplos resueltos paso a paso.
¿Qué es el Álgebra Lineal?
El álgebra lineal es el estudio de vectores, espacios vectoriales, transformaciones lineales y sistemas de ecuaciones lineales. Es una herramienta esencial en muchas disciplinas científicas y técnicas.
También te puede interesar:
Cómo realizar una Suma algebraica
4 Reglas algebraicas básicas
Importancia de Resolver Ejercicios de Álgebra Lineal
Resolver ejercicios de álgebra lineal te ayuda a:
- Comprender los conceptos fundamentales.
- Desarrollar habilidades analíticas.
- Aplicar teorías matemáticas a problemas prácticos.
Ejercicios Resueltos
Sistemas de Ecuaciones Lineales
Ejemplo 1: Sistema de dos ecuaciones con dos incógnitas
Considera el siguiente sistema de ecuaciones: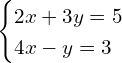
$\begin{cases} 2x + 3y = 5 \\ 4x – y = 3 \end$
Paso 1: Resolver por el método de sustitución
Despejamos $y$ de la primera ecuación:
$y = \frac{5 – 2x}{3}$
Sustituimos $y$ en la segunda ecuación:
$4x – \left(\frac{5 – 2x}{3}\right) = 3$
Multiplicamos todo por 3 para eliminar el denominador:
$12x−(5−2x)=9$
$12x−5+2x=9$
$14x=14$
$x=1$
Sustituimos $x = 1$ en $y = \frac{5 – 2x}{3}$:
$y = \frac{5 – 2(1)}{3} = 1$
La solución del sistema es:
$(x, y) = (1, 1)$
Espacios Vectoriales
Ejemplo 2: Verificación de un subespacio
Sea $V$ el espacio vectorial $\mathbb{R}^3$ y $W$ el conjunto de vectores de la forma $(a, b, 0)$. Verifiquemos si $W$ es un subespacio de $V$.
Paso 1: Verificar el cierre bajo la adición
Tomamos dos vectores cualesquiera $(a_1, b_1, 0)$ y $(a_2, b_2, 0)$ en $W$:
$(a_1, b_1, 0) + (a_2, b_2, 0) = (a_1 + a_2, b_1 + b_2, 0)$
El resultado está en $W$, por lo que está cerrado bajo la adición.
Paso 2: Verificar el cierre bajo la multiplicación escalar
Tomamos un vector $(a, b, 0)$ en $W$ y un escalar $c \in \mathbb{R}$:
$c(a, b, 0) = (ca, cb, 0)$
El resultado está en $W$, por lo que está cerrado bajo la multiplicación escalar.
Como $W$ cumple con ambas propiedades, es un subespacio de $V$.
Transformaciones Lineales
Ejemplo 3: imagen y núcleo de una transformación lineal
Sea $T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ definida por $T(x, y) = (2x + y, x – y)$.
Paso 1: Encontrar el núcleo de $T$
El núcleo de $T$ es el conjunto de vectores $(x, y)$ tales que $T(x, y) = (0, 0)$:
$T(x, y) = (2x + y, x – y) = (0, 0)$
Esto implica que:
$\begin{cases} 2x + y = 0 \\ x – y = 0 \end$
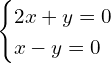
Resolvemos el sistema:
$y = x \\ 2x + x = 0 \implies 3x = 0 \implies x = 0 \\ y = 0$
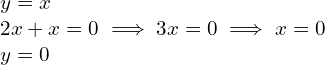
Entonces, el núcleo de $T$ es:
$\{(0, 0)\}$
Paso 2: Encontrar la imagen de $T$
La imagen de $T$ es el conjunto de todos los vectores de la forma $T(x, y) = (2x + y, x – y)$. Para cualquier $(u, v) \in \mathbb{R}^2$, necesitamos encontrar $x$ y $y$ tales que:
$\begin{cases} 2x + y = u \\ x – y = v \end$
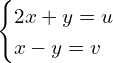
Resolvemos el sistema:
$y = u – 2x \\ x – (u – 2x) = v \implies 3x = u + v \implies x = \frac{u + v}{3} \\ y = u – 2\left(\frac{u + v}{3}\right) = \frac{3u – 2u – 2v}{3} = \frac{u – 2v}{3}$
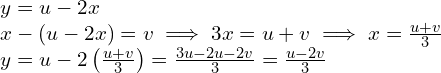
Entonces, la imagen de $T$ es todo $\mathbb{R}^2$, ya que para cualquier $u$ y $v$ existen $x$ y $y$ tales que $T(x, y) = (u, v)$.
Practicar con ejercicios resueltos de álgebra lineal es fundamental para dominar esta disciplina. Aquí en Matemante, te ofrecemos ejemplos claros y detallados que te ayudarán a entender y aplicar los conceptos básicos de manera efectiva. ¡Sigue practicando y mejorando tus habilidades matemáticas!
