Igualdad y desigualdad de conjuntos

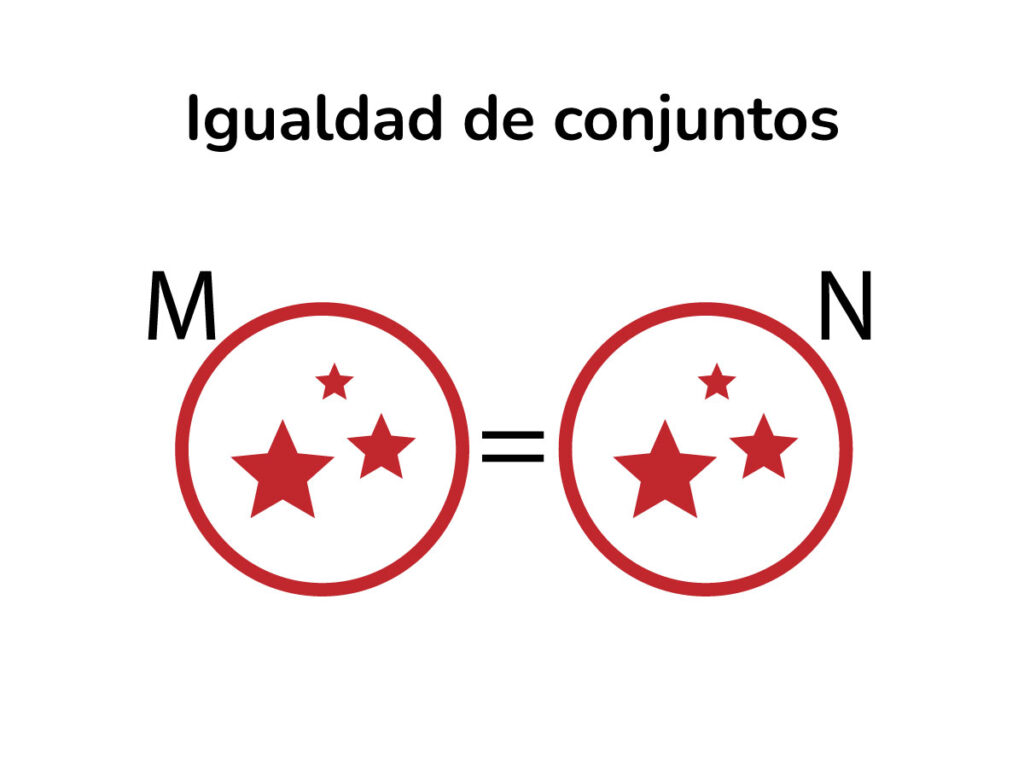
Igualdad de conjuntos

Dos conjuntos son iguales cuando estos tienen los mismos elementos, es decir, que todo elemento de M que pertenece N y todo elemento de N pertenece al conjunto M.

M = N
Si ∀ x ∈ M ⇒ x ∈ N
Si ∀ x ∈ N ⇒ x ∈ M

Propiedades de la igualdad de conjuntos

1. Reflexiva:
   M = M
2. Simétrica:
   Si M = N⇒ N = M
3. Transitiva:
   Si M = N ∧ N = P ⇒ M = P

También te puede interesar:
Teoría de conjuntos – Definición, símbolos y ejemplos
Los subconjuntos y sus propiedades
Símbolos matemáticos con ejemplos de uso

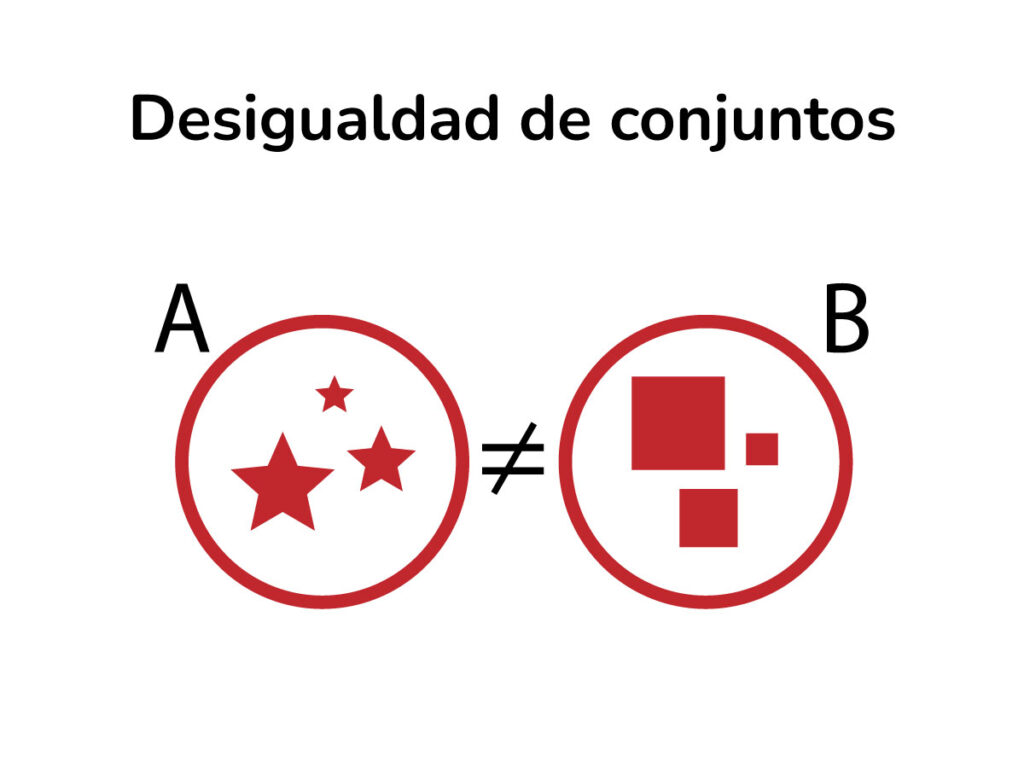
Desigualdad de conjuntos

Llamamos a desigualdad entre conjuntos, a conjuntos formados por todos los elementos que pertenecen a un conjunto A y que no pertenecen a un conjunto B.

A – B = {x | x ∈ A ∧ x ∉ B}

Ejemplo de desigualdad de conjuntos:

A = {1, 2, 3, 4, 5}    B = {4, 5, 6, 7, 8}
A – B = {1, 2, 3}

Propiedades de la desigualdad de conjuntos

1. Si A y B son conjuntos disjuntos, es decir, A ∩ B = Ø, se tiene A – B = A.
2. A ⊂ B entonces A – B = Ø.
3. A – B ≠ B – A
   (A – B) – C ≠ A – (B – C)

¿Tienes alguna duda? No dudes en preguntarme en los comentarios